Number System
Number system is a mathematical notation for representing numbers using different kind of symbols or digits and it allows us to operate arithmetic operations like addition, subtraction, multiplication.
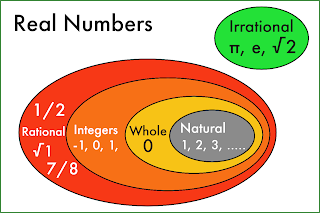
Natural Numbers
The natural numbers are the numbers used for counting and ordering, they are also known as counting numbers and they are represented by N.
e.g ➤ N= 1, 2, 3, 4, 5............ ∞ ( infinite )
Note ➠ zero should not be included
Whole Numbers
When we include zero in natural numbers then it becomes whole number, and we represent it by W.
Whole Number = Zero + Natural Numbers
e.g ➤ W= 0, 1, 2, 3, 4, 5...........∞ ( infinite )
Note ➠ (i) All natural numbers are whole numbers, but not all whole numbers are natural numbers.
(ii) Zero is a whole number, but not a natural number.
Integer Numbers
When we represent whole numbers with positive and negative signs then we call it integer numbers or integers, and we represent it by I.
e.g ➤ I = -∞ ......-3, -2, -1, 0, 1, 2, 3......∞
(i) Positive Integer Numbers
Natural numbers are called positive integer numbers. e.g ➤ 1, 2, 3, 4, ..............
(ii) Negative Integer Numbers
If natural numbers are written with minus sign, then those numbers are called negative integer numbers. e.g ➤ -1, -2, -3, -4, ..............
Rational Numbers
The numbers which can be written in the form of P/Q is called rational numbers.
e.g ➤ 1/2, 3/2, 7/8, √1.........
Where (i) in P/Q, Q ≠ 0
(ii) P and Q are Integers
Irrational Numbers
The number which can not be written in the form of P/Q is called irrational numbers.
Where P and Q are integers and ( Q ≠ 0 )
Note ➠ π is a irrational number but the value of π (3.14) is a rational number.
Real Numbers
A group of rational numbers and irrational numbers is called real numbers, and we represent it by R.
e.g ➤ R= 0, -2, 2/3, -6/15, √2 etc
Imaginary Numbers
Numbers that are not real but just imagined, those are called imaginary numbers.
e.g ➤ √-3, √-15
Note ➠ (i) Thus the square root of these negative numbers cannot be derived.
(ii) They are also written as follows in the language of mathematics (a+ib), (a-ib), (x+iy),(-ix+y), we add I with them and this is very important for higher mathematics.
Even Numbers
Natural numbers which can be completely divided by 2 are called even numbers.
e.g ➤ 2, 4, 6, 8, 10, 12, ............
Commonly these are represent as 2m where m= Natural Number
Odd Numbers
Natural numbers which cannot be completely divided by 2 are called odd numbers.
e.g ➤ 1, 3, 5, 7, 9, ............
Commonly these are represent as 2m - 1 where m= Natural Number
Prime Numbers
All numbers greater than 1, which only can be divided by itself or by 1 are called prime numbers.
e.g ➤ 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ..............
Composite Numbers
All numbers greater than 1, which has at least one divisor other than 1 and itself, is called composite number.
e.g ➤ 4, 6, 9, 15, etc
Co - Prime Numbers
Two natural numbers whose HCF is equal to 1 is called co-prime numbers.
Important Points
Identity Element of Addition
Zero is called identity element of addition because when we add zero to any number it do not change the result.
Identity Element of Multiplication
1 is called identity element of multiplication because when we multiply 1 to any number it do not change the result.
Additive Inverse
Adding a number to the number which make the sum zero is called additive inverse.
Multiplicative Inverse
Multiplying a number to the number which make the product 1, that number is called multiplicative inverse
e.g ➤ Multiplicative inverse of x is 1/x
If you have any doubt or question let me know in the comments.








1 Comments
Nice information
ReplyDelete